Discrete Mathematics for Computer Science

Introduction to Discrete Mathematics for Computer Science

What is Discrete Mathematics?

Discrete mathematics for computer science is a branch of mathematics that deals with distinct, separate values rather than continuous data. Unlike calculus or algebra, which focus on continuous functions and real numbers, discrete mathematics is concerned with structures such as integers, graphs, sets, and logic that have a countable number of elements.

In simple terms, discrete mathematics is the foundation of many computer science concepts, providing essential tools for algorithm design, data structures, and problem-solving techniques. The study of discrete mathematics involves working with mathematical structures that can be counted individually and manipulated in a structured way, making it invaluable for computational logic and software development.

Why is Discrete Mathematics Important in Computer Science?

Discrete mathematics is fundamental to computer science because it lays the groundwork for designing efficient algorithms, managing data, and ensuring secure communications. It provides the mathematical foundation for:

Algorithm Development: Many algorithms rely on principles from discrete mathematics, such as graph theory, combinatorics, and number theory. Sorting algorithms, search algorithms, and network routing algorithms all use discrete structures.
Data Structures: Trees, graphs, stacks, and queues—essential data structures in programming—are based on discrete mathematical concepts. For example, binary trees are used in databases, and graphs are crucial for social network analysis and AI-driven recommendations.
Computer Security & Cryptography: Encryption techniques like RSA and hash functions rely heavily on discrete mathematics, specifically number theory and modular arithmetic, to secure digital transactions and communications.
Artificial Intelligence & Machine Learning: Discrete mathematics is used in logic programming, probabilistic models, and combinatorial optimization problems to make AI systems more efficient and robust.
Networking & Databases: Graph theory helps in designing efficient network routing protocols, while set theory and relational algebra form the basis of database systems like SQL.
Computational Complexity & Automata Theory: Discrete mathematics is used to classify problems based on their computational difficulty and to design finite-state machines, which are crucial in software engineering, compiler design, and natural language processing.

Also Visit: How to Score 95% in Your Exams

Real-World Applications of Discrete Mathematics in Computer Science

To understand the importance of discrete mathematics, let’s look at some real-world applications where it plays a critical role:

Google Search Algorithm: Google’s PageRank algorithm, which determines the relevance of web pages, is based on graph theory, an important topic in discrete mathematics.

Social Media Networks: Platforms like Facebook, Twitter, and LinkedIn use graph theory to represent user connections and recommend friends or followers.

Blockchain & Cryptocurrencies: Bitcoin and Ethereum use cryptographic hashing and modular arithmetic, which are deeply rooted in discrete mathematics, to maintain secure and decentralized ledgers.

Airline & Traffic Navigation: Discrete mathematics is used in optimizing flight schedules, road navigation, and shortest-path algorithms, such as Dijkstra’s algorithm used in Google Maps.

Cybersecurity & Encryption: Public-key cryptography (RSA, ECC) secures online transactions, email communication, and digital signatures, all of which rely on number theory.

Artificial Intelligence & Machine Learning: AI models use combinatorial optimization and graph theory to improve efficiency in tasks such as route optimization and recommendation systems.

Software Development & Compiler Design: Automata theory helps in designing compilers that translate high-level programming languages into machine code.

What Will This Blog Cover?

Now that we’ve established the significance of discrete mathematics in computer science, the rest of this blog will delve into its core topics:

Set Theory – Understanding sets, their properties, and their application in database management and algorithms.
Logic & Propositional Calculus – How logical reasoning helps in software development, AI, and database queries.
Functions, Relations & Algorithms – The backbone of problem-solving in computing.
Combinatorics – How permutations and combinations are used in coding theory and probability analysis.
Graph Theory – The importance of graphs in networking, AI, and web technologies.

This blog will explore these topics in-depth, providing real-world applications, examples, and problem-solving techniques.

Let’s dive into the world of discrete mathematics and uncover its impact on modern computing!

Set Theory in Discrete Mathematics for Computer Science

What is Set Theory?

Set theory is one of the foundational topics in discrete mathematics. A set is a well-defined collection of distinct objects, called elements. These elements can be anything—numbers, letters, symbols, or even other sets.

Set theory provides a mathematical framework to deal with collections of objects and is widely used in computer science for database management, data structures, and logic formulation.

Why is Set Theory Important in Computer Science?

Set theory is crucial in multiple areas of computer science:
Database Systems – SQL and relational databases use set operations like UNION, INTERSECT, and DIFFERENCE to manage data.
Programming & Data Structures – Arrays, hash tables, and collections in programming languages are based on set operations.
Artificial Intelligence & Machine Learning – Clustering, classification, and recommendation systems use sets to group and analyze data.
Theoretical Computer Science – Set theory forms the basis for formal languages, automata theory, and computational complexity.

Basic Terminology in Set Theory

Before we dive deeper, let’s understand some key terms in set theory:

Set (S): A collection of elements, denoted as S = {a, b, c, d}
Element (x): A single item in a set. If x belongs to S, we write x ∈ S
Cardinality (|S|): The number of elements in a set. If S = {1,2,3}, then |S| = 3
Empty Set (∅): A set with no elements, also called the null set. Example: S = {}
Subset (⊆): If every element of A is also in B, then A ⊆ B
Power Set (P(S)): The set of all subsets of S. If S = {1,2}, then P(S) = {∅, {1}, {2}, {1,2}}
Universal Set (U): The set containing all possible elements under discussion.

Set Operations and Their Importance in Computing

In computer science, set operations are widely used in data management, algorithm design, and artificial intelligence. Let’s look at some key operations:

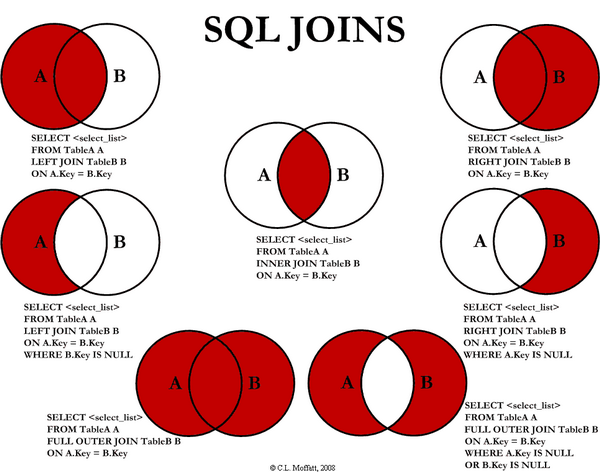
1. Union (A ∪ B)

The union of two sets includes all elements that belong to either A or B.
Example: If A = {1,2,3} and B = {3,4,5}, then A ∪ B = {1,2,3,4,5}

Use Case: In databases, UNION combines results from multiple queries.

2. Intersection (A ∩ B)

The intersection of two sets includes only the elements common to both.
Example: If A = {1,2,3} and B = {3,4,5}, then A ∩ B = {3}

Use Case: Search engines use intersection to match results from multiple search criteria.

3. Difference (A – B)

The difference between sets contains elements in A but not in B.
Example: If A = {1,2,3} and B = {3,4,5}, then A – B = {1,2}

Use Case: Used in spam filtering to differentiate between spam and non-spam emails.

4. Complement (A’)

The complement of a set A contains all elements not in A, relative to a universal set U.
Example: If U = {1,2,3,4,5,6} and A = {1,2,3}, then A’ = {4,5,6}

Use Case: In AI, complements help in negative sampling for training machine learning models.

Applications of Set Theory in Computer Science

1. Databases & SQL Queries
Relational databases use set operations:

UNION combines query results.
INTERSECT retrieves common records.
EXCEPT finds records in one table but not another.

2. Internet & Search Engines
When you search for “Machine Learning AND Deep Learning”, the search engine retrieves only pages that contain both terms (intersection of sets).

3. Machine Learning & AI

In AI, clustering algorithms use set operations to group data.
In natural language processing, sets represent unique words in a document.

4. Networking & Computer Security

Firewalls use set complements to block unwanted IPs.
Cryptographic hash functions use set operations for integrity checks.

Set theory is a fundamental concept that plays a critical role in computing, from designing databases to powering AI algorithms. Understanding how sets work allows developers to build efficient data structures and algorithms.

Next, we will dive into Logic & Propositional Calculus, which forms the basis of decision-making in programming and AI. Stay tuned!

Related

How to Pass Without Studying

Logic and Propositional Calculus in Discrete Mathematics for Computer Science

What is Logic in Computer Science?

Logic is the study of reasoning and the principles that govern valid arguments. In computer science, logic is essential for designing circuits, writing algorithms, creating artificial intelligence, and developing programming languages.

One of the most fundamental forms of logic is propositional logic (or propositional calculus), which deals with statements (propositions) that can be either true (T) or false (F). These logical statements form the basis of computational thinking and decision-making in programming.

Why is Logic Important in Computer Science?

Logic is the backbone of computing systems and artificial intelligence. It plays a crucial role in:

Programming & Software Development – Conditional statements (if-else), loops, and decision-making rely on logical expressions.
Database Queries – SQL uses Boolean logic (AND, OR, NOT) to filter and retrieve data efficiently.
Artificial Intelligence – Logical reasoning helps AI systems like expert systems and chatbots understand and respond to queries.
Digital Circuits & Computer Hardware – Logic gates (AND, OR, XOR, NOT) are fundamental in designing processors and memory storage.
Cybersecurity & Cryptography – Logical proofs help verify encryption and authentication protocols.

Propositional Logic: Basics & Key Concepts

1. Propositions and Truth Values

A proposition is a statement that is either true or false.

Examples of propositions:

“5 is greater than 3.” (True)
“Python is a snake.” (False in a programming context)

2. Logical Operators (Connectives)

Logical operators combine propositions to create more complex expressions.

Operator	Symbol	Meaning	Example
Conjunction	∧	“AND”	(P ∧ Q) is True only if both P and Q are True.
Disjunction	∨	“OR”	(P ∨ Q) is True if at least one of P or Q is True.
Negation	¬	“NOT”	(¬P) inverts the truth value of P.
Implication	→	“If P then Q”	(P → Q) is False only when P is True and Q is False.
Biconditional	↔	“P if and only if Q”	(P ↔ Q) is True when both have the same truth value.

Example:
Let P = “It is raining” and Q = “I carry an umbrella”

Implication: P → Q (If it is raining, then I carry an umbrella.)
Conjunction: P ∧ Q (It is raining, and I carry an umbrella.)
Disjunction: P ∨ Q (Either it is raining, or I carry an umbrella.)

Truth Tables

Truth tables help in understanding how logical operators work.

1. Truth Table for AND (∧)

P	Q	P ∧ Q
T	T	T
T	F	F
F	T	F
F	F	F

Use Case: In database queries, WHERE condition1 AND condition2 returns records satisfying both conditions.

2. Truth Table for OR (∨)

P	Q	P ∨ Q
T	T	T
T	F	T
F	T	T
F	F	F

Use Case: Search engines use OR to return results matching any of the search terms.

3. Truth Table for Implication (→)

P	Q	P → Q
T	T	T
T	F	F
F	T	T
F	F	T

Use Case: In cybersecurity, IF (password is correct) THEN (grant access) follows logical implication.

Logical Equivalences & Laws in Propositional Logic

Logical equivalences simplify expressions, making computations efficient. Some important laws include:

1. De Morgan’s Laws

These laws are crucial for Boolean algebra and circuit design:

¬(P ∧ Q) ≡ ¬P ∨ ¬Q
¬(P ∨ Q) ≡ ¬P ∧ ¬Q

Use Case: Used in digital circuits to simplify NOT gates combined with AND/OR gates.

2. Idempotent Laws

P ∧ P ≡ P
P ∨ P ≡ P

Use Case: Simplifies redundant conditions in programming.

3. Identity Laws

P ∧ True ≡ P
P ∨ False ≡ P

Use Case: Optimizes logical conditions in code execution.

Applications of Logic in Computer Science

1. Programming & Decision-Making
Logical expressions control conditional statements:

if (age > 18 and country == "USA"):
    print("Eligible to vote")

This follows the AND (∧) rule in propositional logic.

2. Digital Circuits & Computer Architecture
Logic gates (AND, OR, NOT) form the basic building blocks of microprocessors and memory units.

3. Artificial Intelligence & Automated Reasoning
AI systems use logical inference to draw conclusions, like in expert systems or chatbot responses.

4. Database Query Optimization
SQL uses logic for filtering data efficiently:

SELECT * FROM students WHERE age > 18 AND city = 'New York';

This uses the conjunction (∧) operator to refine search results.

Logical reasoning is fundamental in computer science, from writing efficient code to designing AI models. Understanding propositional logic allows developers to create error-free algorithms and optimize computational performance.

Next, we will explore functions, relations, and algorithms, which are essential for defining data structures and designing algorithms. Stay tuned!

Functions, Relations, and Algorithms in Discrete Mathematics for Computer Science

In this section, we will explore three crucial concepts in discrete mathematics: functions, relations, and algorithms. These concepts form the backbone of data structures, algorithm design, and database systems in computer science.

1. Functions in Discrete Mathematics

Definition of a Function

A function is a mapping between two sets: a domain (input) and a codomain (output). Every element in the domain is associated with exactly one element in the codomain.

Mathematical Representation:
A function f from set X to set Y is written as:f:X→Yf: X \to Yf:X→Y

where for every x ∈ X, there exists a unique y ∈ Y such that f(x) = y.

Example:
Let X = {1, 2, 3} and Y = {4, 5, 6}. A function f can be defined as:f(1)=4,f(2)=5,f(3)=6f(1) = 4, f(2) = 5, f(3) = 6f(1)=4,f(2)=5,f(3)=6

This means each input from X maps to exactly one output in Y.

Types of Functions

Understanding different types of functions is crucial in computer science, especially in database management, machine learning, and programming.

1. One-to-One (Injective) Functions

A function is one-to-one (injective) if different inputs produce different outputs.f(a)=f(b)⇒a=bf(a) = f(b) \Rightarrow a = bf(a)=f(b)⇒a=b

Example: f(x) = 2x + 3 (Each input maps to a unique output.)

2. Onto (Surjective) Functions

A function is onto (surjective) if every element in the codomain has at least one pre-image in the domain.∀y∈Y,∃x∈X such that f(x)=y\forall y \in Y, \exists x \in X \text{ such that } f(x) = y∀y∈Y,∃x∈X such that f(x)=y

Example: f(x) = x², where Y = [0, ∞). Every output in Y has at least one x in X.

3. Bijective Functions

A function is bijective if it is both injective and surjective. This means every element in the codomain is mapped by a unique element in the domain.

Example: f(x) = x + 1 where X = Y = ℤ (integers). Each input has a unique output, and every possible output has a corresponding input.

Use Case in Computer Science:

Hash Functions (injective functions ensure no two inputs generate the same hash value).
Database Indexing (bijective functions help in efficient data retrieval).

Function Composition and Inverse Functions

Function Composition: (f ∘ g)(x) = f(g(x))
Inverse Function: If f(x) = y, then f⁻¹(y) = x.

Example: If f(x) = x + 5, then f⁻¹(x) = x - 5.

Use Case: Cryptographic algorithms often use inverse functions for encryption and decryption.

2. Relations in Discrete Mathematics

Definition of a Relation

A relation is a set of ordered pairs that define a connection between two sets.

Mathematical Representation:
A relation R from X to Y is a subset of X × Y:R⊆X×YR \subseteq X \times YR⊆X×Y

Example:
Let X = {1, 2, 3} and Y = {a, b, c}. A relation R can be:R={(1,a),(2,b),(3,c)}R = \{(1, a), (2, b), (3, c)\}R={(1,a),(2,b),(3,c)}

This means 1 is related to a, 2 is related to b, and so on.

Types of Relations

1. Reflexive Relation

A relation is reflexive if every element is related to itself.∀x∈X,(x,x)∈R\forall x \in X, (x, x) \in R∀x∈X,(x,x)∈R

Example: The “equal to” relation (x = x) is reflexive.

2. Symmetric Relation

A relation is symmetric if whenever (a, b) ∈ R, then (b, a) ∈ R as well.∀a,b∈X,(a,b)∈R⇒(b,a)∈R\forall a, b \in X, (a, b) \in R \Rightarrow (b, a) \in R∀a,b∈X,(a,b)∈R⇒(b,a)∈R

Example: The “friendship” relation is symmetric because if A is a friend of B, then B is a friend of A.

3. Transitive Relation

A relation is transitive if (a, b) ∈ R and (b, c) ∈ R implies (a, c) ∈ R.∀a,b,c∈X,(a,b)∈R and (b,c)∈R⇒(a,c)∈R\forall a, b, c \in X, (a, b) \in R \text{ and } (b, c) \in R \Rightarrow (a, c) \in R∀a,b,c∈X,(a,b)∈R and (b,c)∈R⇒(a,c)∈R

Example: The “ancestor” relation is transitive because if A is an ancestor of B and B is an ancestor of C, then A is an ancestor of C.

Use Case: Relational databases use relations to link tables (Primary keys & Foreign keys).

3. Algorithms in Discrete Mathematics

What is an Algorithm?

An algorithm is a step-by-step procedure to solve a computational problem.

Characteristics of Algorithms:

Well-defined inputs & outputs
Finite number of steps
Unambiguous instructions
Correctness & efficiency

Types of Algorithms

1. Greedy Algorithms

Solve problems by making the best local choice at each step.
Example: Dijkstra’s Algorithm (Shortest Path).

2. Divide and Conquer

Break a problem into smaller subproblems, solve them recursively, and combine results.
Example: Merge Sort, Quick Sort.

3. Dynamic Programming

Solves problems by breaking them into overlapping subproblems and storing results to avoid recomputation.
Example: Fibonacci sequence, Knapsack problem.

4. Graph Algorithms

Used for network routing, social networks, and AI.
Examples: BFS, DFS, Prim’s Algorithm.

Functions help define transformations in machine learning models.
Relations structure data in databases and networks.
Algorithms provide efficiency in solving complex problems.

Next, we will explore Graph Theory and its applications in computer science. Stay tuned!

Graph Theory and Its Applications in Computer Science

Graph theory is a fundamental area of discrete mathematics that plays a crucial role in various domains of computer science, including networking, artificial intelligence, data structures, and algorithms. In this section, we will cover the essential concepts of graph theory, its types, representations, and real-world applications.

1. Introduction to Graph Theory

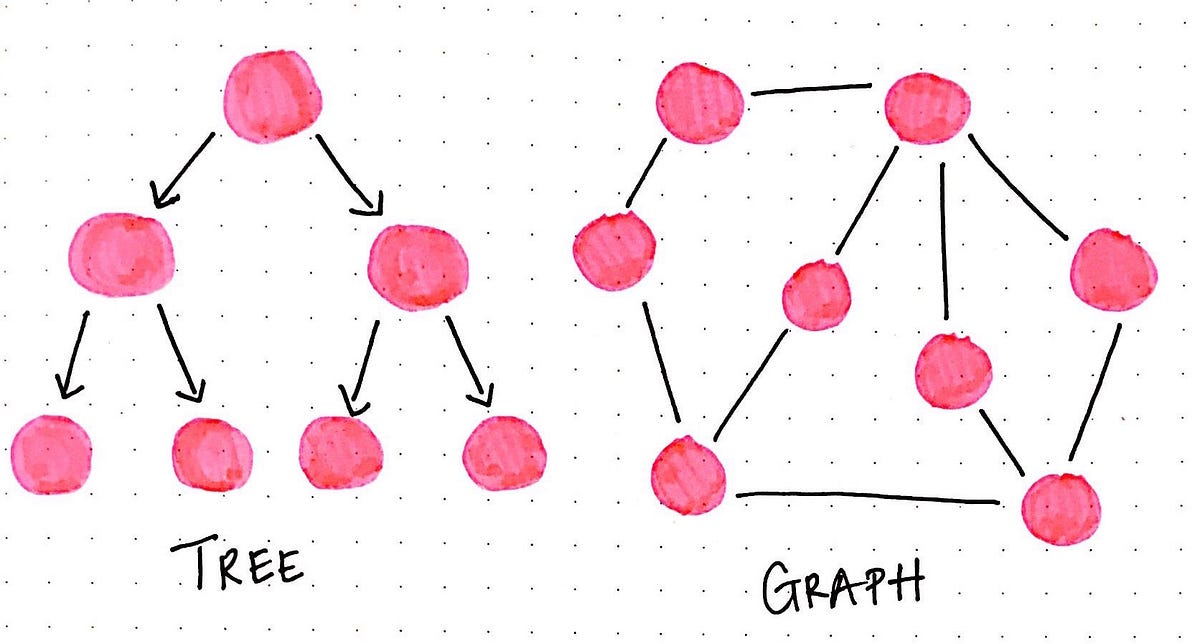
Definition of a Graph

A graph is a mathematical structure used to model pairwise relationships between objects. It consists of:

Vertices (or Nodes): Represent entities.
Edges: Represent the connections or relationships between vertices.

A graph is denoted as:G=(V,E)G = (V, E)G=(V,E)

where:

V is the set of vertices.
E is the set of edges connecting these vertices.

Example of a Graph

Consider a social network where users are represented as nodes, and friendships are represented as edges. If Alice and Bob are friends, there is an edge between their respective nodes.

2. Types of Graphs

Graphs can be classified based on their properties and structures.

1. Directed vs. Undirected Graphs

Directed Graph (Digraph): The edges have a direction, meaning that connections are one-way.
Undirected Graph: The edges do not have a direction, meaning the connection is mutual.

Example:

A Twitter follow network is a directed graph since a user can follow another without reciprocation.
A Facebook friendship network is an undirected graph since friendships are mutual.

2. Weighted vs. Unweighted Graphs

Weighted Graph: Each edge has an associated weight or cost.
Unweighted Graph: All edges have equal weight.

Example:

In a road network, the distance between cities represents edge weights.
A simple social network graph is usually unweighted.

3. Cyclic vs. Acyclic Graphs

Cyclic Graph: Contains at least one cycle.
Acyclic Graph: Contains no cycles.

Example:

A transportation network can have cycles.
A tree (hierarchical structure) is an example of an acyclic graph.

4. Connected vs. Disconnected Graphs

Connected Graph: Every vertex is reachable from any other vertex.
Disconnected Graph: Some vertices are not connected.

Example:

The internet is a connected graph where every device is reachable.
Isolated local area networks form disconnected graphs.

5. Bipartite Graphs

A graph is bipartite if its vertices can be divided into two sets such that no two vertices within the same set are adjacent.

Example:

In a job assignment problem, one set represents jobs and the other represents workers.

3. Graph Representation in Computer Science

1. Adjacency Matrix

An adjacency matrix is a two-dimensional array where:

matrix[i][j] = 1 if there is an edge between vertex i and j.
matrix[i][j] = 0 otherwise.

Example:

For a graph with vertices {A, B, C} and edges {A-B, B-C}, the adjacency matrix is:

	A	B	C
A	0	1	0
B	1	0	1
C	0	1	0

Pros: Fast edge lookup.
Cons: Uses more memory (O(n²)).

2. Adjacency List

An adjacency list stores a list of adjacent nodes for each vertex.

Example:

A → [B]
B → [A, C]
C → [B]

Pros: Memory-efficient.
Cons: Slower edge lookup than an adjacency matrix.

3. Incidence Matrix

An incidence matrix represents the relationship between vertices and edges.

Example:

For edges {A-B, B-C}, the incidence matrix is:

	Edge1 (A-B)	Edge2 (B-C)
A	1	0
B	1	1
C	0	1

4. Fundamental Graph Algorithms

Graph algorithms are essential for solving problems in networking, AI, and optimization.

1. Breadth-First Search (BFS)

BFS explores a graph level by level, making it useful for shortest path problems in unweighted graphs.

Algorithm

Start at a given node.
Visit all adjacent nodes.
Move to the next level and repeat.

Time Complexity: O(V + E)
Applications: Shortest path in unweighted graphs, social network analysis.

2. Depth-First Search (DFS)

DFS explores as far as possible along each branch before backtracking.

Algorithm

Start at a node.
Visit a neighbor and go deeper recursively.
If no neighbors are left, backtrack.

Time Complexity: O(V + E)
Applications: Cycle detection, maze solving.

3. Dijkstra’s Algorithm (Shortest Path)

Dijkstra’s algorithm finds the shortest path from a source node to all other nodes in a weighted graph.

Algorithm

Assign infinite distance to all nodes except the source.
Select the node with the smallest distance.
Update distances of adjacent nodes.
Repeat until all nodes are processed.

Time Complexity: O((V + E) log V) using a priority queue.
Applications: GPS navigation, network routing.

4. Floyd-Warshall Algorithm

Finds the shortest paths between all pairs of vertices in a weighted graph.

Time Complexity: O(V³)
Applications: Network optimization, routing tables.

5. Prim’s Algorithm (Minimum Spanning Tree)

Finds the minimum cost spanning tree of a connected, weighted graph.

Time Complexity: O((V + E) log V)
Applications: Network design, circuit design.

6. Kruskal’s Algorithm (Minimum Spanning Tree)

Finds the minimum spanning tree by sorting edges by weight and adding them sequentially while avoiding cycles.

Time Complexity: O(E log E)
Applications: Power grid optimization.

5. Applications of Graph Theory in Computer Science

Graph theory is widely used in various areas of computer science.

1. Computer Networks

Graphs model network topology.
Routing algorithms like Dijkstra’s optimize data transfer.

2. Social Networks

Social platforms use graphs to model connections.
Algorithms detect influential users and communities.

3. AI and Machine Learning

Graph neural networks (GNNs) analyze relationships in data.
AI uses graphs for knowledge representation.

4. Web Crawlers

The internet is a vast graph where pages are nodes.
Web crawlers use BFS to index web pages.

5. Compiler Design

Dependency graphs help optimize code execution.
Control flow graphs represent program logic.

6. Game Development

AI pathfinding uses A* and Dijkstra’s algorithms.
Game maps are modeled as graphs for navigation.

7. Cybersecurity

Attack detection uses graph algorithms to identify malicious connections.
Network monitoring detects anomalies in traffic.

Graph theory is a foundational topic in discrete mathematics with profound implications in computer science. From data structures to network routing and AI, graphs are used to solve complex problems efficiently. Understanding graph algorithms and their applications is crucial for software developers, data scientists, and engineers.

In the next section, we will explore combinatorics and probability in discrete mathematics and their significance in algorithm analysis and cryptography.

Conclusion

Discrete mathematics provides a foundation for various fields such as computer science, engineering, and logic. By studying topics like set theory, combinatorics, graph theory, and algorithms, students gain problem-solving skills and a deeper understanding of the mathematical principles underlying digital systems and software. The importance of discrete math continues to grow in areas like cryptography, network design, and artificial intelligence, highlighting its relevance in modern technology. Mastery of these concepts equips students with the tools needed to approach complex real-world problems with logic and precision.